Shufflix: Design Summary

Background

In the late 1990s machines for duplicating bridge boards had become affordable for individual districts under DBF or even for individual clubs. This resulted in a demand for a version of the bridge dealing software that could be distributed freely without jeopardizing the quality of the boards dealt. This version of KG was released in 1998 as freeware. At this time, a standard for interchanging information relating to duplicate bridge, including deals, was evolving. This effort, driven by Tis Veugen, resulted in the Portable Bridge Notation, which was also supported in the 1998 version of KG.

During 1998 and 1999, prompted by problems similar to those experienced in Denmark in 1989, Hans van Staveren took the initiative to develop dealing software for the Dutch Bridge Federation and the WBF with the intention of achieving a quality that can be used worldwide for serious as well as everyday tournaments. This effort has resulted in Bigdeal, which is a state of the art dealing program that anyone may download and run on their own computer.  This initiative touched off several discussions on the Internet about the requirements that such software must meet and the possible designs that can meet these requirements.

As a spin-off of these discussions, Alesia Software has developed Shufflix, which is a WWW-based state-of-the-art dealing program that provides deals for a session of bridge in a matter of seconds using only a WWW browser.

Requirements

• Statistics (strong). The deals generated must be statistically indistinguishable from deals chosen at random.  [This property is known as unbiased in the cryptographic literature about random number generators]
• Non-repeating (strong). A sequence of boards generated for one event must not be observably related to the boards generated for some other event.  [This property is another requirement from the cryptographic literature concerning random number generators]
• Clerically robust (medium). The software must support clerical procedures that help prevent inadvertent use of generated deals in an event that they were not intended for.
• Unpredictable (medium). No one, not even the programmer, possibly assisted by ample computer power, should be able to predict the deals of a tournament before the event.    [This property also appears as a requirement from the cryptographic literature concerning random number generators]
• No discernable pattern (weak). It must not be possible for an honest, but knowledgeable player to predict the rest of the deals to be played during a session, given the deals already played.
• Users (weak): Few and trusted. Only a small number of known users will have versions of the software.
• Auditable (medium). It must be possible to ascertain after the event that the deals were not intentionally modified after dealing.

• No discernable pattern (medium). It must not be possible for dishonest, knowledgeable players with access to covert computer resources of large but reasonably limited capacity to predict the rest of the deals to be played during a session, given the deals already played.
• Users (medium): Potentially Hostile vs. Protected. A large community of general users must be supported without threatening the integrity of selected, specially protected users.

• Unpredictable (strong). It must be infeasible, even when backed by immense, but realistic computing resources, to categorically rule out that any given sequence of boards will be generated for a particular event.
• No discernable pattern (strong). It must not be possible for dishonest, knowledgeable players, even when backed by immense, but realistic computing resources, to predict the rest of the deals to be played during a session, given the deals already played.
• Users (strong): Potentially Hostile Mutually Protected. A large community of potentially hostile users must be protected against each others' use of the software.
• Auditable (strong). It must be possible to ascertain after the event that the deals were not intentionally modified during and after dealing.

Oh, by the way, there is also Hackix. This is a 9-line Perl program that shows what a programmer who is only worried about the statistics requirement might develop. The requirements analysis of Hackix is another way of getting to grips with what these requirements are all about.

Overall Design of Shufflix

• A Tournament Description, which gives the name and date of the event for which the deals are intended and the number of boards to be generated.
• A file of unpredictable information, called the entropy, using a term from information theory.

The Entropy

• For reasonably serious tournaments, it can be desirable to demonstrate that dishonest participants backed with immense computer power cannot predict the deals, but where the operator of the dealing software is trusted, special care is needed to acquire entropy file.  Shufflix accomplishes this by extracting 128 unpredictable bits from the device urandom on the Linux operating system, which constitues Shufflix's platform.

The Output

Step 1: Generate the Run Seed

The computer entropy consists of these contributions:

• 128 bits read from the Linux device /dev/urandom on the web server www.alesia.dk. This contribution is unpredictable at a cryptographically strong level; it is based on timings of interrupts within the kernel. The use of /dev/urandom was suggested by Alan Jaffray. This contribution is enough on its own to ensure that the run seed is cryptographically unpredictable. The contribution from the user makes it more unpredictable, but only slightly so.
• All user-specific information available to the server, including the wall clock time, the user's IP address, and the process number of the server process. This information does add a little to the overall entropy of the run seed, but a significant effect is to ensure that even if the entropy is reused in another run (which would be an error), the runseed will be based on different input to the hash function, and therefore be different.

Step 2: Generate a Sequence of Pseudo-Random Bytes

The overall approach, which is recommended in Carl Ellison's paper on Cryptographic Random Numbers is to concatenate the unpredictable runseed with a sequence counter and process that through the hash function. This yields 16 bytes for each call.

Step 3: Generate Boards

Step 3 shuffles the cards once for each board, using the random bytes from step 2.  The algorithm selects a card at random and moves it to the top of a result pile, repeating until all 52 cards have been moved.  To do this, a random byte is converted to random number of appropriate size K by taking its remainder modulo K.  To avoid bias, the entire byte is discarded if it is larger than the largest multiple of K less than or equal to 256.

The resulting deals are described using 52 characters for each. Here is an example of such a file.

#Y:6c423d24150bcff21b2ae9a23e5c208d #I:Example session #K:20 #T:2001-09-02 18:55:17 Z #D:2001-02-11 #V:Shufflix 0.9 ## 0101221003211322031120130332300213312002130230321231 2113323201003002231331301113003321222111222203010030 0212322021303333210310012132210021310031130010233122 1121312013100110320332023320130333220011123210322002 1332003013022112100012113233113213301032220012003223 3221310312202231001113321302301211301330222000103023 2101121210202033032332101020012220133110021133332033 3032210011133200011000213132321333222130311012022023 2202013011221233032031033313002201123012011013120323 2101332112010122133230100100223330130020012333311222 3311011230111312133232032310302203203222120000112030 1113020310202020302311332131223233212303211001000213 1310220230013203233001212230330313012011220013223111 0133222002333301221211033233211101121000013012203023 2102300100120210001132121332202233231133333021102031 3230130221101031332303031332212221001302011103221020 2130000213212201321202033323221030213120330311010113 3123302001332200011020121333121232302301122033011021 1013221010302303020323333220030131011001321213122212 1300323212211033331212321100003122031102301022312003

Each line after the Tournament Description describes a board. The number 0,1,2, and 3 signify North, East, West, and South, respectively. The first character shows which hand is to get the A, the next character shows who gets the K, and so on through the s, the s, the s, and the 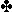s, ending with the 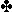2. This format is named .tso in honor of Thomas Andrews (thomaso), who uses this format in generating his Impossible Book of Bridge Deals.

Step 4: Generate Various Output Formats

• HTML in Danish and English
• DUP for the Duplimate machine
• PBN for interchange with other bridge software

Generally, anyone can write post-processing software that formats the deals as they see fit. The best candidate for further formatting is PBN because it is in general use for interchanging bridge software. Otherwise, the easiest format to decode is probably the .tso format. For a fairly straightforward example, see the Perl program tso-dup.pl.

It is important to support the clerical processes surrounding the use of the deals, so whenever possible, the Tournament Description should be carried over to the new format. For this reason, formats like the .DUP format, which discards the Tournament Description, should be used only when absolutely necessary, e.g. when feeding the deals to a Duplimate machine.

Source Code

It is an important property of Shufflix that public access to the source code in no way invalidates the properties of the software. On the contrary, openness to public scrutiny should support overall trust in the Shufflix software.

Requirements Coverage

Statistics (strong).

Of course, the theory is useless unless the implementation actually fulfills the statistical requirements. So validation is called for. In KG, this was achieved by creating 4000 runs of 40 boards (that is 160 000 boards), counting various statistics, and performing a chi-square test against the theoretical distribution of these statistics. The statistics can be quite varied, and outsiders are invited to invent statistical challenges. Typical examples are

• which hand gets the 7?
• how many boards with a void per run of 36 boards?
• where is the K when the AQJ are in one hand?

The statistical tests still use 4000 sequences of 40 boards each (160 000 boards).  The sequences are generated along the following lines:

• Both the entropy and the Tournament Identification are selected without operator intervention.
• The Tournament Identification is generated systematically.
• The entropy was picked up from the www.random.org, which makes entropy publicly available on the WWW.

Non-repeating (strong)

And if that should fail, the run seeds going to be different with extreme high likelihood, and that also makes it absolutely unlikely that two different events get related boards.

[Statistical note: Since there are 2**128 different run seeds, the probability that two specific runs of Shufflix use the same run seed is 1/2**128.  More importantly, the Birthday Paradox implies that even when Shufflix has run 2**64 times, the probability that some run seed has been used more than once is less than ½.  2**64 is a huge number; if every person on Earth (less than 2*33 persons on Earth) runs Shufflix once a second (less than 2**25 seconds in a year) it still takes more than 64 years (2**6 years) to reach 2**64 runs.]

A feature of step 2 in the algorithm is that even if the same 16 random bytes are output by MD5 in two different runs, the previous and subsequent bytes in the two runs will still be completely unrelated. Again, this is due to the properties of the one-way hash function.

Clerically Robust (medium)

Unpredictable (strong)

No Discernable Pattern (strong)

Users (strong): Potentially Hostile Mutually Protected

Someone else might generate the same sequence of boards by dishonest design. The entropy ensures against that: The dishonest user has to guess a 128-bit number in order to generate the same boards. That is sufficient protection in practice.

Auditable (strong)

Auditing that the run seed was not selected knowingly in order to create deals with certain properties is more complicated.  See the FAQ for a discussion.

Overall Secrecy

For a specific event, the entropy and all the output from steps 1 through 4 have to be kept secret until the boards have been played. Of course, this is no different from any other mechanism for dealing for a bridge tournament, including manual dealing and manual duplication.

The simplest precaution is to deal the boards just in time - that way very few people have a chance to know anything about the boards before it is too late.

Shufflix uses HTTPS to ensure that alle information regarding the deals is encrypted when transmitted over the internet.

Version 2017-09-26/ jbc